Nota: Esta entrada forma parte de un conjunto de materiales dirigidos a los participantes en algunos ciclos de talleres que realizamos eventualmente con la finalidad de facilitar el trabajo personal y de transformación. El propósito de estos textos es servir de punto de partida para la preparación, reflexión y trabajo previo al taller. Utilizaremos este conjunto de entradas a modo de biblioteca desde la que poder acceder a estos materiales siempre que se necesiten. Si has llegado a esta página por casualidad y te resulta de interés, nos alegramos y te invitamos a revolver entre nuestro contenido.
A continuación, ofrecemos unas breves notas en lenguaje profano para intentar exponer los aspectos elementales de la octava, tal y como se utilizan en el lenguaje musical, y que resultan necesarios para comprender la ley de octavas descrita por Ouspensky. Vayan por adelantando mis disculpas por todas las inexactitudes que, sin duda, las personas con formación musical encontrarán en esta explicación, redactada por un verdadero analfabeto musical.
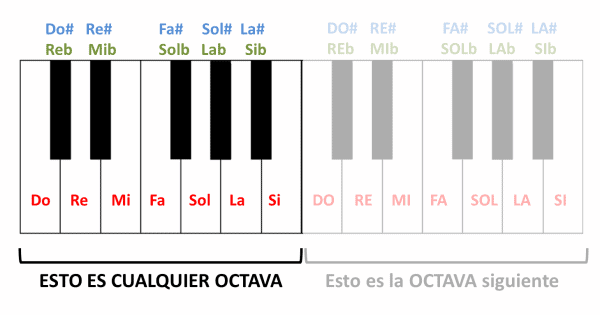
Empecemos por lo más simple. A todos nos suena que la escala musical tiene 7 notas: del Do al Si, y luego se vuelve a repetir el Do. Pues bien, estas 7 notas forman una octava, ya que desde el primer Do al segundo Do hay 8 notas, si las contamos a las dos.
Octava en un teclado de piano (ilustración obtenida de www.ciudadpentagrama.com)
Por otra parte, sabemos que el sonido en general, y las notas musicales, en particular, consisten en una rápida oscilación del aire, capaz de propagarse a través del espacio ocupado por dicho aire en la forma de una onda de presión que vibra a una frecuencia determinada (la frecuencia será el número de veces que dicha onda vibra en un segundo). Cuanta mayor sea la frecuencia, más energía tiene la onda y más agudo percibiremos el sonido. Así, desde un punto de vista más formal, la octava musical se puede definir como el intervalo que separa dos notas musicales cuyas frecuencias están en relación 2 a 1. Es decir, que una es el doble de la otra. En la siguiente figura se muestran las frecuencias de las notas de una octava musical, en la que se puede comprobar como el Do de la octava superior tiene una frecuencia que es igual exactamente al doble de la frecuencia del Do de la escala anterior.

Frecuencias de la 4ª octava (ilustración obtenida de www.ciudadpentagrama.com)
Debido a esta relación entre las frecuencias de las notas, existe una fuerte correspondencia entre las mismas notas de escalas diferentes, hasta el punto de presentar un sonido similar, aunque una suene más aguda que la otra. Es por eso que, si una determinada melodía se interpreta con las mismas notas pero en una octava superior, sonará igual, en el sentido de que se tratará exactamente de la misma melodía, aunque con un sonido más agudo.
Si observamos el teclado de un piano, comprobaremos que las siete notas de una octava están siempre localizadas en las teclas blancas, mientras que las negras están reservadas para los semitonos. Veamos qué significa eso:
Dicho de una manera de andar por casa, un tono sería la diferencia de tonalidad (más agudo o más grave) que existe entre dos notas consecutivas “en la mayoría de los casos” como sucede, por ejemplo, entre el Do y el Re. Como podemos imaginar, un semitono sería la mitad de un tono. En el caso del teclado del piano, esto se traduce en que las teclas negras siempre están separadas por un semitono de las teclas blancas adyacentes. Están, por así decirlo, a mitad de camino en tonalidad entre dichas teclas blancas.
Sin embargo, también podemos ver que, en la manera en que las teclas se distribuyen en un teclado a lo largo de una octava, existe una cierta irregularidad. Esto es debido a que la distancia en frecuencia entre dos notas consecutivas de una octava no es siempre la misma. Concretamente, la distancia entre Mi y Fa y entre Si y Do (de la octava siguiente) es la mitad que entre el resto de las notas. Es decir, la distancia entre estos pares de notas es de un semitono, en lugar de un tono completo. En el teclado del piano, estas notas corresponden con esos pares de teclas blancas entre las cuales no existe una tecla negra.
Esto es lógico si pensamos que, en el teclado del piano, la distancia entre dos teclas consecutivas, independientemente de su color, es siempre de un semitono. Así, mientras que entre Do y Re existe una tecla negra, correspondiente al semitono entre ellas dos, entre Mi y Fa no habrá tal tecla ya que, al estar separadas solamente por un semitono, “ya no cabe” una tecla negra entre ellas. Y lo mismo ocurre entre Si y Do de la siguiente octava.
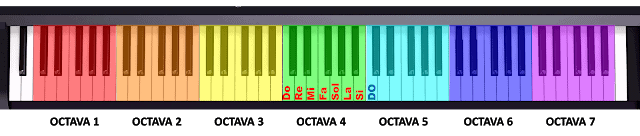
Octavas en un piano (ilustración obtenida de www.ciudadpentagrama.com)
Otra manera de imaginar la octava es como una escalera, no de 7, sino de 12 peldaños, en la que cada nota estuviera escrita en la superficie de un peldaño, siendo la separación entre dos escalones consecutivos de un semitono, e igual para todos los escalones. Entonces, para recorrer las notas de la octava mientras subimos la escalera, necesitaríamos ir pasando los escalones de dos en dos, con la excepción de los pasos de Mi a Fa y de Si a Do, que requerirían subir únicamente un escalón. Dicho de otra manera, una octava tiene 7 notas pero 12 semitonos.
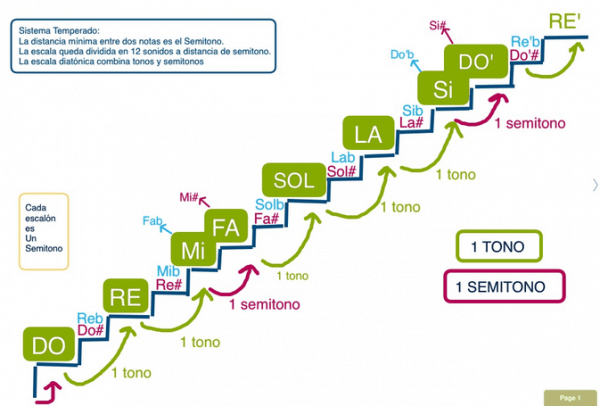
En esta imagen, la altura de cada escalón correspondería a un semitono. Y la altura entre dos escalones, sería un tono completo. (ilustración obtenida de https:/www.mariajesusmusica.com)
Así, cuando hablemos de semitonos en cualquier proceso analizado desde el punto de vista de la ley de los Siete, nos estaremos refiriendo a los intervalos correspondientes entre las etapas 3 y 4 (notas Mi y Fa) y entre la etapa 7 y la primera del siguiente ciclo (Si y Do) de dicho proceso.





Deja tu comentario